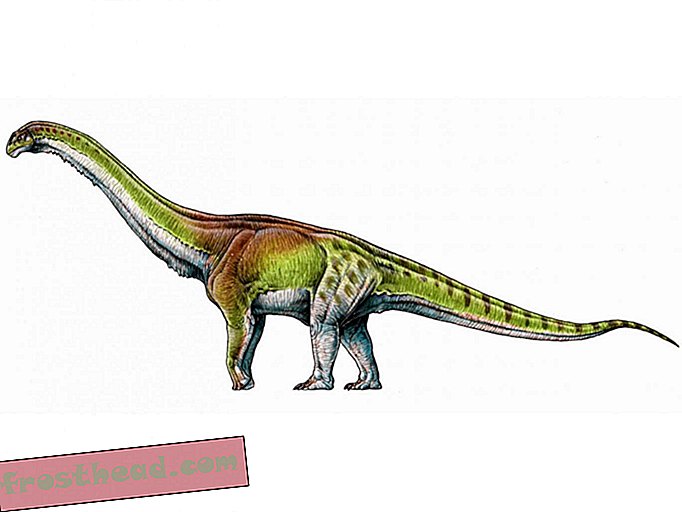
14. maaliskuuta ei ole säännöllinen pi-päivä tänä vuonna. Matematiikan harrastajat juhlivat tapahtumaa Ultimate Pi Day -tapahtumana, koska päivämäärä vastaa pi: n viittä ensimmäistä numeroa (3.1415) kuin vain kolme ensimmäistä. Tätä matemaattista yhtymäkohtaa ei tapahdu uudelleen vuosisadan ajan, 14. maaliskuuta 2115.
Asiaan liittyvä sisältö
- Maailma on täynnä piirejä
Pi ( π ), joka on määritelty ympyrän ympärysmitan suhteena sen halkaisijaan, on sekä transsendenttinen että irrationaalinen luku, tarkoittaen sitä ei koskaan voida kirjoittaa kahden kokonaisluvun suhteena, ja se jatkuu loputtomiin ilman mitään toistuvaa kuviota. Pi ei ole ainoa irrationaalinen luku - siellä on myös esimerkiksi Eulerin numero (e) ja kultainen suhde ( φ tai phi). Mutta se on edelleen kiehtovan lähteen luonne, koska sen alkuperä on helposti selitettävissä, sanoo Mary Livio, astrofysiikka tutkijalta Space Telescope Science Institute Marylandissa.
”Jokainen voi ymmärtää kuinka pi johdetaan. Kaikki muut numerot ovat monimutkaisempia. Esimerkiksi numero phi sisältää tietyn viivan jaon, ja luku e vaatii, että sinun on tiedettävä, mikä on logaritmi ”, sanoo Livio, kirjan kirjoittaja Onko Jumala matemaatikko?
Toinen suuri osa pi: n vetoomuksesta on, että sillä on tuntematon tapana esiintyä matemaattisissa kaavoissa, joista monet ovat tärkeitä arjen prosesseissa kuvankäsittelystä GPS-navigointiin. Tässä on vain pieni näyte yleisimmin käytetyistä kaavoista, jotka sisältävät pi:
Fourier-muunnos
Tämä matemaattinen työkalu, joka on nimetty ranskalaisen matemaatikon Jean-Baptiste Joseph Fourier'ksi, hajottaa signaalin komponenttitaajuuksilleen - pikemminkin kuin kuinka musiikillinen sointu voidaan jakaa komponenttien nuotteihin. Pohjimmiltaan Fourier-muunnokset ovat ihanteellisia aaltopohjaisten signaalien, kuten äänen tai valon, käsittelyyn ja kuvioiden löytämiseen. Se tekee Fourier-muutoksesta keskeisen työkalun nykyaikaisessa digitaalimaailmassa.
Sitä on kutsuttu yhdeksi tärkeimmäksi algoritmiksi, jonka ihmiskunta on koskaan kehittänyt. Nyt se saattaa olla hyperbole, mutta ehkä se ei ole ”, sanoo Glen Whitney, New Yorkin kansallisen matematiikkamuseon perustaja ja johtaja. Fourier-muunnelmia käytetään koko ajan puhdistamaan digitaalisia kuvia, pop-tähtijen automaattiseen virittämiseen ja etsimään kaukana muita tähtiä kiertäviä planeettoja. Työkalu on tärkeä myös ääni-teksti -ominaisuuksissa, jotka ovat nyt älypuhelimien vakiovarusteita. ”Kun käytät Siriä tai Google Nyt, yksi ensimmäisistä vaiheista on ottaa äänesi ja tehdä siitä Fourier-muunnos… osoittautuu, että vokaalien tunnistaminen on paljon helpompaa, kun katsot niiden Fourier-muunnelmia kuin kun katsot alkuperäiset signaalit itse ”, Whitney sanoo.
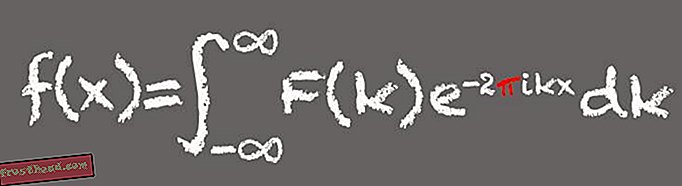(Kuva Victoria Jaggard) Pi esiintyy Fourier-muunnoksessa, koska yksi kaavan komponenteista tai lausekkeista liittyy siniiniin ja kosiniin ja ympyrän ympäri kulkevan hiukkasen muodostamiin kulmiin. "Aina kun sinulla on kaava, joka käsittelee ympyröitä tai kulmia, et tule yllättymään, kun pi näkyy", Whitney sanoo.
Heisenbergin epävarmuusperiaate
Yksi kvantimekaniikan pilareista, Heisenbergin epävarmuusperiaate, toteaa, että tarkkailija ei voi tietää samanaikaisesti sekä alaatomisen hiukkasen sijaintia että nopeutta. Sen sijaan mitä tarkemmin partikkelin sijainti tunnetaan, sitä vähemmän voidaan tietää sen nopeudesta.
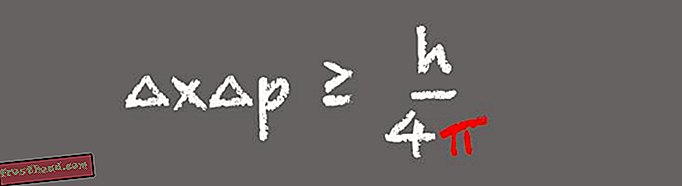(Kuva Victoria Jaggard) Pi: n esiintyminen Heisenbergin epävarmuusperiaatteessa on järkevää, kun huomaat, että kaavassa asema ja vauhti ovat Fourier-muunnoksia toisistaan, Whitney sanoo. Epävarmuusperiaate on tärkeä nykymaailmassa, koska se kuvaa valohiukkasten eli fotonien käyttäytymistä kuituoptisissa viestintäjärjestelmissä. ”Se kertoo meille, että emme voi tietää sekä fotonien sijaintia että vauhtia äärimmäisen tarkasti. Et voi suunnitella viestintäprotokollia, jotka rikkovat Heisenbergin epävarmuusperiaatetta, koska ne eivät toimi. "
Stoken laki
Stoken laki laskee voiman, joka tarvitaan pienen pallon - ts. Kolmiulotteisen ympyrän - siirtämiseen viskoosisen nesteen läpi tietyllä nopeudella. Sillä on sovelluksia aloille, jotka ovat maantieteellisiä ja lääketieteellisiä.
(Kuva Victoria Jaggard) "Laki koskee nimenomaan viskositeetin vaikutusta nestepallossa", Whitney kertoo, miten pi tulee peliin. Mitä Stoken lakia käytännössä käytetään, älä katso kauemmas kuin autosi. "Vuosikymmenien ajan tapa varmistaa, että yritykset varmistivat moottoriöljylläsi oikean viskositeetin autollesi, oli pudottaa kirjaimellisesti sarja testipalloja öljyyn ja mitata aika, joka kuluu niiden putoamiseen nesteen läpi", Whitney kertoo. Nykyään tavallisimpaan tapaan mitata öljyn viskositeetti sisältyy kapillaariputken viskosimetriksi kutsuttu työkalu, jota ei tarvita palloja, mutta tulos ilmoittaa silti mittayksiköissä, joita kutsutaan sentistokeiksi.
Eulerin kaava
Tämän kaavan versio, joka on nimetty sveitsiläisen matemaatikon Leonard Euleriksi, sisältää pi: n, ja se kerää yhteen mielenkiintoisimmat numerot matematiikassa yhdestä paikasta:
(Kuva Victoria Jaggard) ”Kaikki vain ajattelevat tämän olevan uskomatonta. Kaikki nämä numerot, joita pidämme erityisinä, esiintyvät yhdessä kauniissa yhtälössä ”, Livio sanoo. Vaikka tämä hieno kaava voi herättää kunnioitusta matemaatikoissa, yhtälön hyödyllisempi muoto on hiukan pidempi:
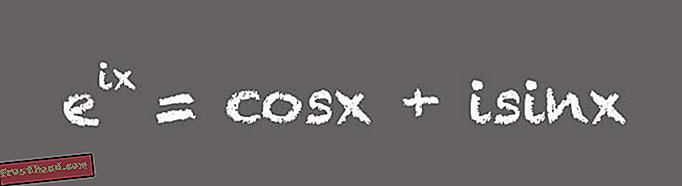(Kuva Victoria Jaggard) Tämä pakkaamaton versio Eulerin kaavasta on uskomaton työkalu, Whitney sanoo. Esimerkiksi, se on tärkeää suunniteltaessa elektroniikkaa, joka käyttää vaihtovirtaa tai vaihtovirtaa. ”Laajennetussa muodossa olevan Eulerin kaava tarkoittaa, että voit käyttää monimutkaisia tai kuvitteellisia numeroita analysoimaan ja suunnittelemaan vaihtovirtapiirejä”, Whitney kertoo. Tämä johtuu siitä, että vaihtovirtapiirissä jännite on määrä, joka värähtelee ajan kuluessa - tyypillisesti 60 kertaa sekunnissa, esimerkiksi tavanomaisessa Yhdysvaltain sähkövirralla. "Eulerin kaavan täysi versio opettaa, kuinka voimme käyttää monimutkaisia numeroita kätevänä pikakuvana värähtelevien ilmiöiden mallintamiseen", Whitney sanoo.
Einsteinin kenttäyhtälöt
Albert Einsteinin kenttäyhtälöt ovat hänen yleisen suhteellisuusteoriansa ydinosa, joka kuvaa kuinka massasta ja energiasta tuleva painovoima luo avaruus-ajan kaarevuuden.
(Kuva Victoria Jaggard) "Kaarevuuden kuvaaminen sisältää geometrian, ja koska pi: n alkuperäinen määritelmä tulee geometriasta, sen ulkonäkö tässä yhtälössä ei ole niin yllättävää", Livio sanoo. Sen lisäksi, että paljastetaan perustavanlaatuinen totuus maailmankaikkeuden toiminnasta, sen lisäksi, että suhteellisuusteorialla on monia käytännön sovelluksia. Esimerkiksi satelliittit, jotka muodostavat navigointiin käytettävän globaalin paikannusjärjestelmän, olisivat toivottomasti synkronoituneita keskenään, jos insinöörit eivät ota huomioon teorian ennustamia ajan dilaatiovaikutuksia.
