Tämä artikkeli on päivitetty alkuperäisestä viestistä, joka ilmestyi 14. maaliskuuta 2013.
Asiaan liittyvä sisältö
- Naimisiin Pi-päivänä on asia
- "Presidentinpäivää" ei oikeastaan ole olemassa
14. maaliskuuta, kirjoitettuna numerolla 3/14, edustaa pi (π) kolme ensimmäistä numeroa, mikä on ympyrän kehän suhde sen halkaisijaan. Maailman kuuluisimman matemaattisen vakion muistamiseksi harrastajat ympäri maailmaa omaksuvat sisäisen kurjuutensa viettämällä Pi-päivää. Päivämäärä - joka sattuu olemaan myös Einsteinin syntymäpäivä - inspiroi erilaisia tapahtumia joka vuosi. Tänä viikonloppuna järjestetään perimmäinen Pi-päivä, koska vuoden lisääminen päivämäärämerkintöihimme, 3/14/15, sisältää vielä enemmän numeroita järjestyksessä. Emme saa niin paljon pi uudelleen 100 vuotta.
Miksi ihmiset ovat hulluja pi? Luku - 3, jota seuraa lakkaamaton satunnaislukujono desimaalin jälkeen, on irrationaalinen, mikä tarkoittaa, että sitä ei voida ilmaista jakamalla kaksi kokonaista numeroa. Se on myös transsendentaalinen luku, mikä tarkoittaa, että se ei ole minkään algebrallisen numeron juuri. Tämä irrationaalinen ja transsendenttinen luonne vetoaa ihmisiin, ehkä siksi, että pi: n jatkuva numerovirta heijastaa loputonta ympyrää, jonka se auttaa jäljittämään.
Pi on pitänyt melkein mystistä laatua ihmisille koko ajan. Sen lausumaton läsnäolo voi tuntua Stonehengen pyöreissä raunioissa, kupolitettujen Rooma-temppelien holvattuissa kattoissa sekä Platonin ja Ptolemaioksen taivaanpiireissä. Se on inspiroinut vuosisatojen matemaattisia arvoituksia ja joitain ihmiskunnan kuvauksellisimpia teoksia. Ihmiset viettävät vuosia elämästään yrittäessään muistaa sen numerot ja järjestämään kilpailuja nähdäkseen kuka tietää eniten numeroita desimaalin jälkeen. Jotkut kirjoittavat "piaku" - runot, joissa kirjainten lukumäärä jokaisessa sanassa edustaa seuraavia pi-numeroita. Vielä toiset luovat monimutkaisia taideteoksia, jotka ovat saaneet vaikutteita pi satunnaisuudesta. Lista jatkuu ja jatkuu, kuten itse pi.
Tässä on joitain merkittäviä hetkiä pi: n historiassa:
1900-1650 eKr
Vaikka termiä pi ei ollut vielä käytössä, babylonialainen tabletti antoi arvon ympyrän kehän suhteesta sen halkaisijaan 3, 125, mikä ei ole huono! Eräässä toisessa asiakirjassa Rhind Papyrus, egyptiläinen kirjoittaja kirjoitti: "Leikkaa 1/9 halkaisijaltaan ja rakenna neliö lopulle; tällä on sama alue kuin ympyrä." Tämä tarkoittaa, että pi on 3, 16049, mikä on myös melko tarkka, Rutgersin yliopiston matematiikan laitoksen David Wilsonin mukaan.
800-200 eKr
Raamatun kohdat kuvaavat Salomonin temppeliin rakennettua seremoniallista uima-allasta: "Hän teki merestä valettua metallia, pyöreän muodon, mitattuna kymmenen kyynärää reunasta vanteen ja viiden kyynärän korkeudella. Mittaamiseen kului kolmenkymmenen kyynärän viiva. sen ympärillä." (I Kings 7: 23-26.) Tämä asettaa pi: n vain 3: een.
250 eKr
Syrakusan Archimedes lähestyi pi: n arvoa etsimällä kahden muodon alueet - 96-puolinen monikulmio, joka on merkitty ympyrään ja yksi piirretty sen ulkopuolelle. Monikulmioiden alueet kerrosivat ympyrän pinta-alaa antaen Archimedesin ylä- ja alarajat halutulle suhteelle. Vaikka hän tiesi, ettei hän ollut löytänyt pi: n tarkkaa arvoa, hän pystyi asettamaan sen välille 3.1408 - 3.1429.
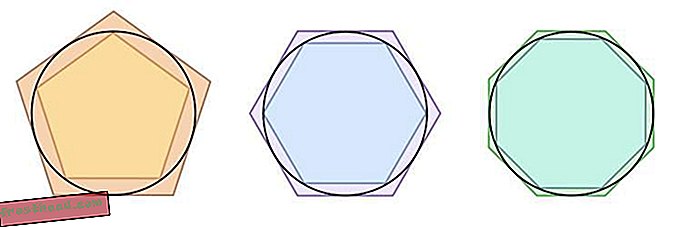("Archimedes pi", Leszek Krupinski - Oma työ. Lisensoitu CC BY-SA 3.0: n kautta Wikimedia Commonsin kautta) 1300-luvun lopulla
Intialainen matemaatikko ja Sangamagraman tähtitieteilijä Madhava oli ensimmäinen ennätys, jonka mukaan pi voitaisiin edustaa ehtojen kokonaisuutena äärettömässä järjestyksessä - esimerkiksi 4 - 4/3 + 4/5 - 4/7 + 4/9 - 11.4 .. ∞. Hänen ponnistelut tuottivat arvon pi: lle, joka oli oikein 13 desimaalin tarkkuudella, ja hän auttoi luomaan joitain perustaa laskennan kehittämiselle.
1706
Walesin matemaatikko William Jones alkoi käyttää merkkiä π ympyrän kehän ja halkaisijan suhteessa. Kuuluisa sveitsiläinen matemaatikko Leonhard Euler otti tämän käytön käyttöön vuonna 1737 auttaen sitä popularisoimaan teoksillaan.
1873
Englantilainen amatöörimatemaatikko William Shanks laskee pi 707 numeroon. Hänen numero oli kirjoitettu pyöreän huoneen seinälle - nimeltään Pi-huone - Palais de la Découvertessa, ranskalaisessa tiedemuseossa. Mutta hänen numeronsa oli oikea vain 527. numeroon. Virhe havaittiin lopulta vuonna 1946 ja korjattiin seinällä vuonna 1949.
1897
Indianan lakia säätäjät lähettävät melkein laskun, joka muuttaa virheellisesti pi arvon kiinteäksi 3.2. Amatöörimatemaatikon Edwin Goodwinin seurauksena Indianan yleiskokous esitteli House Bill 246: n, joka tarjosi "uuden matemaattisen totuuden" valtion käyttöön ilmaiseksi. Väitetyn totuuden oli Goodwinin yritys neliön ympyrä - palapeli, joka edellyttää, että saman alueen ympyrä ja neliö rakennetaan käyttämällä vain geometrista kompassia ja suoraviivaista. Lakiesitys hyväksyttiin yksimielisesti parlamentissa, mutta senaatti - ja siten myös valtio - säästyi hämmennykseltä, jonka purdue-matematiikan professori CA Waldo joutui olemaan valtionhuoneessa sinä päivänä. "Näytti laskun ja tarjosi johdannon nerolle, jonka teoria se oli. Waldo kieltäytyi sanomasta, että hän tunsi jo tarpeeksi hulluja ihmisiä", Tony Long of Wired kirjoitti. Waldo antoi senaattoreille matematiikan opetuksen, ja lasku kuoli.
1988
Larry Shaw San Franciscon Exploratoriumista esittelee ensimmäisen Pi-päivän juhlan.
2005
Chao Luista, sitten jatko-opiskelijasta Kiinassa, tulee Guinnessin ennätyksen haltija puhuttaessa pi: hän laski numeron 67 980 numeroon 24 tunnissa ja 4 minuutissa (kilpailusäännöt edellyttivät, että korkeintaan 15 sekuntia voi kulkea minkä tahansa kahden numeron välillä).
2009
Pi päivästä tulee kansallinen tapahtuma! Tennessenen demokraattinen kongressiedustaja Bart Gordon esitteli yhdessä 15 tukijan kanssa HR 224: n, joka "tukee Pi-päivän nimeämistä ja sen viettämistä ympäri maailmaa; tunnustaa National Science Foundationin matematiikan ja luonnontieteiden koulutusohjelmien jatkuvan merkityksen ja kannustaa koulut ja opettajat tarkkailevat päivää sopivilla toimilla, jotka opettavat opiskelijoille Pi: tä ja kiinnostavat heitä matematiikan opiskeluun. " Edustajainhuone hyväksyi päätöslauselman kyseisen vuoden 12. maaliskuuta osoittaen, että pi-rakkaus on puolueetonta.
Kuinka juhlit Pi-päivää?
